Задача
Докажите неравенство (1 + x1)...(1 + xn) ≥ 2n, где x1...xn = 1.
Значения переменных считаются положительными.
Решение
Раскрыв скобки в левой части, мы получим сумму 2n слагаемых, каждое из которых есть произведение нескольких переменных. Эти слагаемые разбиваются на 2n–1 пар взаимно обратных чисел (например,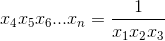 
). Сумма чисел в каждой паре согласно неравенству Коши не меньше 2. Значит, вся сумма не меньше 2n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет