Задача
Докажите неравенство xαyβ≤ αx+ βy для положительных значений переменных при условии, что α + β = 1 (α, β > 0).
Решение
Пусть xαyβ > αx + βy для некоторых x, y и α. При этих значениях x и y f(α) = xαy1–α – αx – (1 – α)y – непрерывная функция. Значит, она больше нуля на некотором интервале, содержащем α. Этот интервал содержит положительное рациональное число
r = k/n. Положим m = n – k. По выбору r f(r) > 0, то есть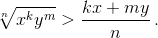 
Но это противоречит неравенству Коши (см. задачу 161404 а).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет