Задача
Докажите, что для чисел {xn} из задачи 161297 можно в явном виде указать разложения в цепные дроби: xn+1 = [1;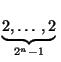
].
Оцените разность |xn – 
|.
Решение
Подходящие дроби Pk/Qk к разложению = [1; (2)] в цепную дробь удовлетворяют рекуррентным соотношениям P–1 = 1, P0 = 1, Pk = 2Pk–1 + Pk–2;
Q–1 = 0, Q0 = 1, Qk = 2Qk–1 + Qk–2 (см. задачи 160613, 160601). Отсюда по индукции легко вывести соотношения Pk = Qk + Qk–1; 2Qk = Pk + Pk–1.
Пусть xn = Pk/Qk, где k = 2n–1 – 1. Дробь xn+1 получается из дроби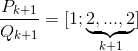 
заменой последней двойки на 1 + Pk/Qk. По аналогии с формулой из решения задачи 160616 имеем
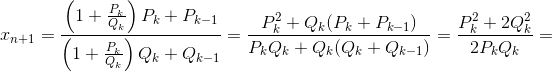
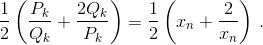
Таким образом, {xn} – последовательность из задачи 61297.
Поскольку Qk > 2Qk–1 при k > 2, то Qk > 2k.
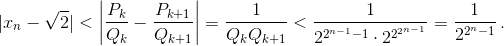
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь