Задача
Докажите при помощи комплексных чисел, что композицией двух гомотетий является гомотетия или параллельный перенос: 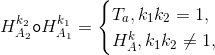 причём в первом случае вектор a параллелен прямой A1A2, а во втором случае центр результирующей гомотетии A лежит на прямой A1A2 и k = k1k2.
Здесь
причём в первом случае вектор a параллелен прямой A1A2, а во втором случае центр результирующей гомотетии A лежит на прямой A1A2 и k = k1k2.
Здесь 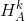 обозначает гомотетию с центром в A с коэффициентом k.
обозначает гомотетию с центром в A с коэффициентом k.
Решение
Композиция гомотетий 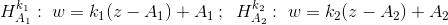 имеет вид w = k1k2z + k2(1 – k1)A1 + (1 – k2)A2.
имеет вид w = k1k2z + k2(1 – k1)A1 + (1 – k2)A2.
Если k1k2 = 1, то получаем параллельный перенос. Если же k1k2 ≠ 1, то это гомотетия с коэффициентом k1k2, центр A которой находится из уравнения k1k2z + k2(1 – k1)A1 + (1 – k2)A2 = k1k2(z – A) + A.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет