Задача
Известно, что z + z–1 = 2 cos α.
а) Докажите, что zn + z–n = 2 cos nα.
б) Как выражается zn + z–n через y = z + z–1?
Решение
а) Если z + z–1 = 2 cos α, то и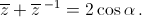 
Вычитая, получим 
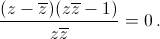Значит, либо 
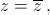то есть z – действительное число, либо |z| = 1. Первый случай возможен только при z = ± 1 (иначе |z + z–1| > 2 ≥ 2 cos α). Во втором случае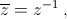 
то есть Re z = cos α. Отсюда z = cos α ± i sin α, и по формуле Муавра zn + z–n = 2 cos nα. б) zn + z–n = (cos α + i sin α)n + (cos α – i sin α)n =
= 
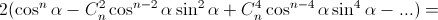
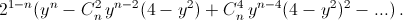
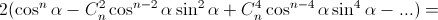
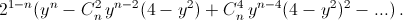
Ответ
б)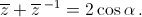 
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет