Решение задачи отсутствует

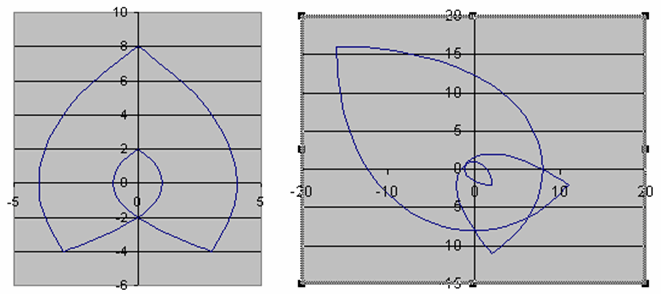
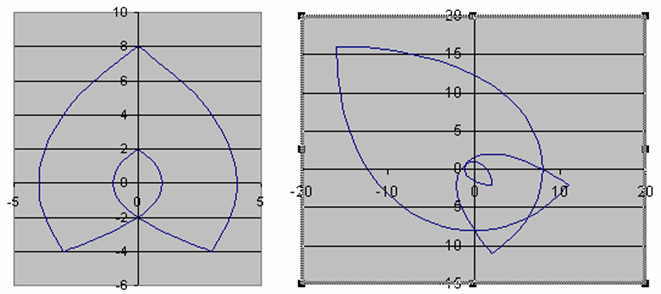
Движется a) против часовой стрелки по параболе  x=  ^y2/₄– 1  от точки  (0, 2)  до точки  (3, –4),  потом по параболе  x= 4 –^y2/₁₆  от точки  (3, –4)  до точки  (0, 8),  затем по параболе  x=^y2/₁₆– 4  от точки  (0, 8)  до точки  (–3, –4)  и по параболе  x= 1 –^y2/₄  от точки  (–3, –4)  до точки  (0, 2)  (рис. слева);

б) против часовой стрелки по кривой  (t³– 3t, 1 – 3t²)  (–1 ≤t≤ 2),  потом по кривой  (8 – 6t², 12t–t³)  (–1 ≤t≤ 2),  затем по кривой (t³– 12t, 6t²– 8)  (–1 ≤t≤ 2)  и по кривой  (3t²– 1, 3t–t³)  (–1 ≤t≤ 2)  (рис. в центре); в) по часовой стрелке по окружности  x²+ (y– ½)²= ¼  от точки  (– ½, ½)  до точки  (–²/₅,¹/₅),  потом по окружности  (x– ¼)²+y²=¹/₁₆  от точки  (–²/₅,¹/₅)  до точки  (¼, – ¼),  затем по окружности  x²+ (y– ¼)²=¹/₁₆  от точки  (¼, – ¼)  до точки  (–¹/₅, –²/₅)  и по окружности  (x+ ½)²+y²= ¼  от точки  (–¹/₅, –²/₅)  до точки  (– ½, ½)  (рис. справа).