Задача
Периодом дроби 1/7 является число N = 142857. Оно обладает следующим свойством: сумма двух половин периода – число из одних девяток
142 + 857 = 999). Докажите в общем случае, что для простого q > 5 и натурального p < q период дроби p/q есть такое 2n-значное число N = N1N2, что N1 + N2 = 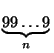 .
.
Решение
Пусть t = 2n – длина периода. Согласно
задаче 770881, выполняется сравнение 10t ≡ 1 (mod q). Отсюда 10n ≡ – 1 (mod q) и p/q + {10n·p/q} = 1. Но в десятичной системе эти дроби имеют вид p/q = 0,N1N2, 10n·p/q = 0,N1N2, поэтому N1 + N2 = 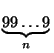 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет