Задача
Докажите утверждение обратное тому, что было в задаче 160668:
если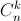 
делится на n при всех 1 ≤ k ≤ n – 1, то n – простое число.
Решение
Пусть n – составное число и p – один из его
простых делителей.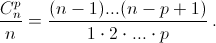 
В числителе нет множителей,
кратных p, а в знаменателе – есть. Следовательно, это число – не целое, то есть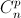 
не делится на n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет