Задача
Докажите, что если квадратное уравнение с целыми коэффициентами имеет корень [![]() ], то вторым корнем служит число
], то вторым корнем служит число 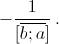
Решение
Корень α квадратного уравнения с целыми коэффициентами имеет вид 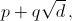 где p и q рациональны, а d – натуральное число "без квадратов" (в его разложение все простые множители входят в первой степени). Так как представление иррационального числа в таком виде единственно, то из формулы корней квадратного уравнения следует, что второй корень равен
где p и q рациональны, а d – натуральное число "без квадратов" (в его разложение все простые множители входят в первой степени). Так как представление иррационального числа в таком виде единственно, то из формулы корней квадратного уравнения следует, что второй корень равен 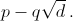 Это значит, что квадратное уравнение с корнем α единственно с точностью до множителя.
Это значит, что квадратное уравнение с корнем α единственно с точностью до множителя.
Как показано в решении задачи 160623, число α = [![]() ] является корнем уравнения bx² – abx – a = 0. Пусть β – второй корень этого уравнения. Тогда
] является корнем уравнения bx² – abx – a = 0. Пусть β – второй корень этого уравнения. Тогда 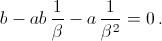 Это значит, что
Это значит, что 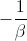 является положительным корнем уравнения ax² – abx – b = 0, то есть (согласно той же задаче 60623)
является положительным корнем уравнения ax² – abx – b = 0, то есть (согласно той же задаче 60623) 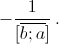
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь