Задача
а) Докажите, что положительный корень квадратного уравнения bx² – abx – a = 0, где a и b – различные натуральные числа, разлагается в чисто периодическую цепную дробь с длиной периода, равной 2.
б) Верно ли обратное утверждение?
Решение
Число α, заданное периодической цепной дробью [
], удовлетворяет соотношению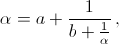 
которое легко приводится к виду
bα² – abα – a = 0. Таким образом, α и является положительным корнем данного квадратного уравнения.
Ответ
б) Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет