Задача
Докажите, что если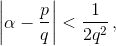 
то p/q – подходящая дробь к числу α.
Решение
Можно считать, что α > 0.
Предположим сначала, что α – число иррациональное и Pn/Qn – подходящие дроби к α. В этом случае последовательность знаменателей стремится в бесконечность, значит для некоторого n будут выполнены неравенства Qn ≤ q < Qn+1. Предположим, что p/q ≠ Pn/Qn. Тогда число p/q попадает в один из трёх интервалов (– ∞, Pn/Qn), (Pn/Qn, Pn+1/Qn+1), (Pn+1/Qn+1, ∞) (будем считать, что n чётно, то есть Pn/Qn < Pn+1/Qn+1).
В первом случае из неравенств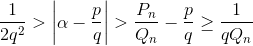 
следует оценка Qn > 2q, которая противоречит выбору n.
Во втором случае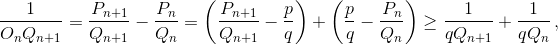 
откуда q ≥ Qn + Qn+1, что также противоречит выбору n.
В третьем случае из неравенств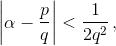 
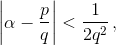получаем оценки
Qn+1 > 2q и 1 ≤ q/Qn+1 + Qn/2q. Отсюда 1 < q/2q + q/2q = 1.
Таким образом, ни один из этих трёх случаев невозможен, и p/q = Pn/Qn.
Пусть теперь α рационально. Тогда α = Pn/Qn для некоторого n. Если q < Qn, то вышеприведенные рассуждения можно повторить.
Если же q ≥ Qn, но p/q ≠ Pn/Qn, то из неравенств 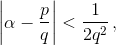получаем 2q < Qn. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь