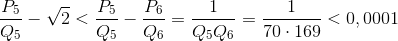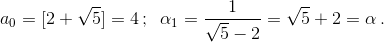а) Разложение числа     в цепную дробь известно из задачи 160613, подходящие дроби вычислены в замечании к задаче 160614. Поскольку     (см. задачу 160602), то подходит дробь  ^P₅/_Q5 = ⁹⁹/₇₀.   б) Разложим число   α = 2 +   в цепную дробь.     Следовательно,  α = [4, (4)].  Вычисляя подходящие дроби, получаем  P₃ = 305,  Q₃ = 72,  Q₄ = 305.  Поскольку  Q₃Q₄ > 10000,  подходит дробь  ^P₃/_Q3 = ³⁰⁵/₇₂.   в) Разложим число  β = 3 +   в цепную дробь.     

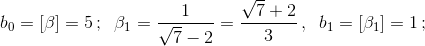
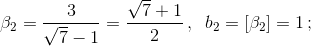
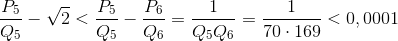
Следовательно,  β – 1 = [4, (1, 1, 1, 4)],  а  β = [5, (1, 1, 1, 4)].  Вычисляя подходящие дроби, получаем  P₇ = 271,  Q₇ = 48,  Q₈ = 223.  Поскольку

Q₇Q₈ > 10000,  подходит дробь  ^P₇/_Q7 = ²⁷¹/₄₈.

а) ⁹⁹/₇₀;   б) ³⁰⁵/₇₂;   в) ²⁷¹/₄₈.