Докажем сначала, что всякая чисто периодическая цепная дробь  α = [a₀; a₁, ..., a_k–1, α]  задаёт квадратичную иррациональность. При решении задачи 160601 а) была получена формула, которая выражает зависимость подходящей дроби от последнего неполного частного. Заменяя в этой формуле a_k на α, приходим к равенству 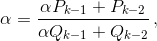    которое дает квадратное уравнение для α:  α²Q_k–1 + α(Q_k–2 – P_k–1) – P_k–2 = 0.  Таким образом, α – квадратичная иррациональность.

  Осталось заметить, что если α – квадратичная иррациональность, а  β = [b₀; b₁, ..., b_m, α],  то β также является квадратичной иррациональностью.

Ответ задачи отсутствует