Задача
Найдите все взаимно простые a и b, для
которых 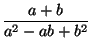 = 3/13.
= 3/13.
Решение
Из условия видно, что a + b кратно 3. Тогда и a² – ab + b² = (a + b)² – 3ab кратно 3. Значит, a + b делится на 9. Рассмотрим два случая.
1) a и b положительны. Тогда 13(a + b) = 3(a + b)² – 9ab ≥ 3(a + b)² – 9/4 (a + b)² = 3/4 (a + b)², откуда a + b ≤ 52/3.
Следовательно, a + b = 9, (a + b)² – 3ab = 13, ab = 14, то есть {a, b} = {7, 2}.
2) a > 0, b ≤ 0. Тогда a ≥ 9, 13(a + b) = 3(a² – ab + b²) ≥ 3a² ≥ 27a ≥ 27(a + b). Противоречие.
Ответ
{7, 2}.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет