Задача
При каких целых n сократимы дроби
а) 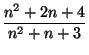 ; б)
; б) 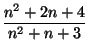 ?
?
Решение
а) Так как (n² + 2n + 4, n2 + n + 3) = (n + 1, 3), то дробь будет сократима, когда (n + 1, 3) = 3. б) Так как (n³ – n² – 3n, n² – n + 3) = (n² – n + 3, 6n), то дробь можно сократить либо на 2, либо на 3, либо на некоторый делитель числа n. Первый случай невозможен так как число n2 – n + 3 всегда нечётно. Во втором случае n должно равняться 3k или 3k + 1. В третьем случае
(n² – n + 3, n) = (n, 3), поэтому n снова должно быть числом вида 3k.
Ответ
а) При n = 3k – 1; б) при n = 3k и n = 3k + 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет