Олимпиадная задача о треугольнике и центре вписанной окружности

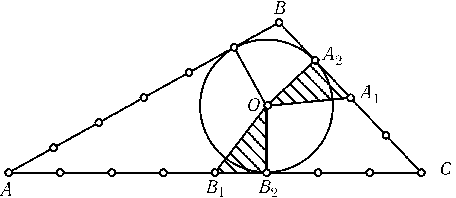
Не обязательно. Докажем, что центр Oвписанной окружности треугольникаABCсо сторонамиAB= 6,BC= 4 и CA= 8 одинаково удален от середин сторонACи BC. Обозначим середины сторонACи BCчерез B₁и A₁, а основания перпендикуляров, опущенных из точки OнаACи BC, — через B₂и A₂(рис.). Так какA₁A₂= 1 =B₁B₂(см. задачу 3.2) и OA₂=OB₂, то$\triangle$OA₁A₂=$\triangle$OB₁B₂т. е.OA₁=OB₁.

Ответ задачи отсутствует