Задача
Дан выпуклый пятиугольник, все углы которого тупые. Докажите, что в нем найдутся две такие диагонали, что круги, построенные на них как на диаметрах, полностью покроют весь пятиугольник.
Решение
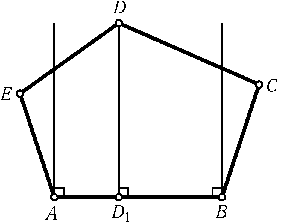
ПустьAB — наибольшая сторона пятиугольника. Рассмотрим полосу, заданную перпендикулярами к сторонеAB, проведенными черезAиB. Так как углыEABиABCтупые, точкиEиCлежат вне этой полосы. Поэтому точкаDлежит внутри полосы, так как иначе длина одного из отрезковEDиDCбыла бы больше длины отрезкаAB. Обозначим проекцию точкиDна отрезокABчерезD1(рис.). Тогда круги с диаметрамиADиBDполностью покрывают четырехугольникиAEDD1иBCDD1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет