а) Предположим, что из нескольких попарно различных по величине квадратов сложен прямоугольник. Рассмотрим самый маленький квадратQ. С одной из его сторон имеет общую часть сторона некоторого большего квадратаA. Сторона квадратаAвыходит за пределы стороны квадратаQ. Образовавшийся угол должен быть заполнен некоторым квадратомB, сторона которого снова больше стороны квадратаQ. Получаем ещё один угол, который должен быть заполнен квадратомC, а затем ещё один угол, который должен быть заполнен квадратомD. При этом между квадратамиAиDне может быть к колодцак (т.е. квадратыAиDдолжны иметь общую границу), поскольку иначе для заполнения к колодцак потребовался бы квадрат, который меньше самого маленького квадратаQ. Итак, если из пяти попарно различных по величине квадратов можно сложить прямоугольник, то мы знаем, как они должны быть сложены: самый маленький квадрат находится в центре, а к нему примыкают четыре других квадрата, образуя следующую конфигурацию (или симметричную ей):

Пустьq,a,b,c,d— длины сторон квадратов. Тогдаa=b+q,b=c+q,c=d+q,d=a+q. Сложив эти равенства, получим 5q= 0. Этого не может быть. б) Продолжим решение задачи а), пользуясь тем, что там уже доказано. Мы уже знаем, как должны быть расположены самый маленький квадрат и прилегающие к нему квадраты. Поэтому если из шести попарно различных квадратов можно сложить прямоугольник, то они должны быть расположены так: Но тогда у квадратовDиEесть общая стороны, поэтому они равны. А по условию все квадраты попарно различны.

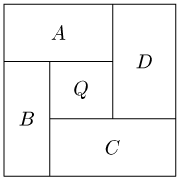
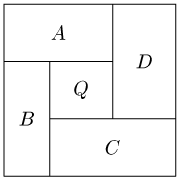
Ответ задачи отсутствует