Задача
а) Докажите, что приn= 2kсреди полученных фигур не более 2k- 1 углов. б) Может ли приn= 100 среди полученных фигур быть только три угла?
Решение
а) Все точки пересечения данных прямых можно заключить в некоторую окружность. Прямые разбивают эту окружность на 4kдуг. Ясно. что две соседние дуги не могут одновременно принадлежать углам, поэтому число углов не превосходит 2k, причем равенство может достигаться, только если дуги. принадлежащие углам, чередуются. Остается доказать, что равенство не может достигаться. Предположим, что дуги, принадлежащие углам, чередуются. Так как по обе стороны от любой из данных прямых лежит по 2kдуг, то противоположные дуги (т. е. дуги, заданные двумя прямыми) должны принадлежать углам (рис.), чего не может быть.
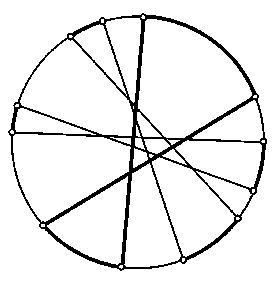
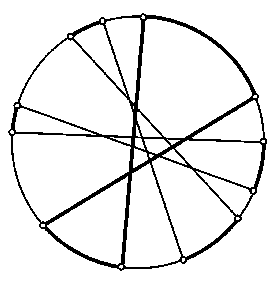
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь