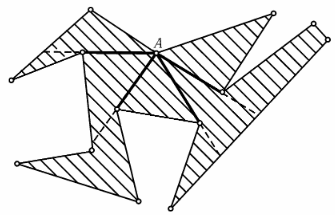
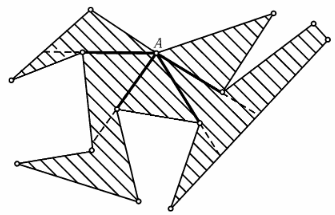
а) Если многоугольник выпуклый, то утверждение очевидно. Предположим теперь, что внутренний угол многоугольника при вершине A больше 180°. Видимая часть стороны видна из точки A под углом меньше 180°, поэтому из точки A видны части по крайней мере двух сторон. Следовательно, существуют лучи, выходящие из точки A, на которых происходит смена (частей) сторон, видимых из точки A (на рис. изображены все такие лучи). Каждый из этих лучей задаёт диагональ, целиком лежащую внутри многоугольника.

б) Из рис. видно, как построить n-угольник, у которого ровно  n – 3  диагонали лежат внутри его. Остаётся доказать, что у любого n-угольника есть по крайней мере  n – 3  диагонали. При  n = 3  это утверждение очевидно. Предположим, что утверждение верно для всех k-угольников, где  k < n,  и докажем его для n-угольника. Согласно а) n-угольник можно разрезать диагональю на два многоугольника:  (k+1)-угольник и (n–k+1)-угольник, причём  k + 1 < n  и  n – k + 1 < n.  У них имеется соответственно по крайней мере  (k + 1) – 3  и  (n – k + 1) – 3  диагоналей, лежащих внутри. Поэтому у n-угольника имеется по крайней мере  1 + (k – 2) + (n – k – 2) = n – 3  диагонали, лежащих внутри.

Ответ задачи отсутствует