Первый способ. Предположим, что точка X построена. Пусть B' – точка, симметричная точке B относительно прямой MN; окружность радиуса AB' с центром B' пересекает прямую MN в точке C (из двух точек пересечения выбираем лежащую от прямой BB' по ту же сторону, что и точка A). Тогда луч B'X является биссектрисой угла AB'A'. Следовательно, X – точка пересечения прямых MN и B'K, где K – середина отрезка AC.

  Второй способ. Строим окружность с центром в точке B, касающуюся прямой MN. Из точки A', симметричной A относительно MN, проводим касательную A'D к этой окружности (из двух касательных выбираем ту, для которой точка касания D находится по одну сторону с A относительно перпендикуляра, опущенного из B на MN). Тогда X – точка пересечения A'D и MN. Действительно,

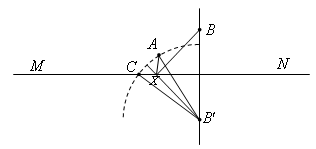
∠AXM = ∠A'XM = ∠DXN = 2∠BXN.

Ответ задачи отсутствует