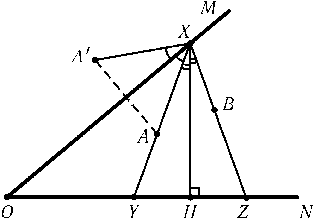
Пусть проекция точки Aна прямуюONлежит ближе к точке O, чем проекция точки B. Предположим, что равнобедренный треугольникXYZпостроен. Рассмотрим точку A', симметричную точке Aотносительно прямойOM. Опустим из точки XперпендикулярXHна прямуюON(рис.). Так как$\angle$A'XB=$\angle$A'XO+$\angle$OXA+$\angle$YXH+$\angle$HXZ= 2$\angle$OXY+ 2$\angle$YXH= 2$\angle$OXH= 180^o- 2$\angle$MON, то уголA'XBизвестен. Точка Xявляется точкой пересечения прямойOMи дуги, из которой отрезокA'Bвиден под углом180^o- 2$\angle$MON. При этом проекция точки Xна прямуюONдолжна лежать между проекциями точек Aи B. Обратно, если$\angle$A'XB= 180^o-$\angle$MONи проекция точки Xна прямуюONлежит между проекциями точек Aи B, то треугольникXYZравнобедренный.

Ответ задачи отсутствует