Предположим, что четырехугольникABCDпостроен. Для определенности будем считать, чтоAD>AB. Пусть O — центр вписанной окружности; точка D'симметрична Dотносительно прямойAO;A' — точка пересечения прямыхAOи DC,C' — точка пересечения прямыхBCи A'D'(рис.). В треугольникеBC'D'известны сторонаBD'и прилегающие к ней углы$\angle$D'BC'= 180^o-$\angle$Bи $\angle$BD'C'=$\angle$D. Построим треугольникBC'D'по этим элементам. Так какAD'=AD, то можно построить точку A. Затем строим точку Oпересечения биссектрис угловABC'и BD'C'. Зная положение точки O, можно построить точку Dи вписанную окружность. Точка Cявляется точкой пересечения прямойBC'и касательной к окружности, проведенной из точки D.

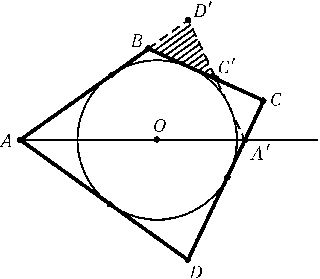
Ответ задачи отсутствует