Задача
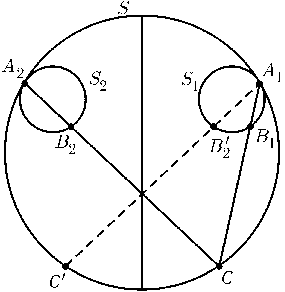
Равные окружности S1и S2касаются окружности Sвнутренним образом в точках A1и A2. Произвольная точка Cокружности Sсоединена отрезками с точками A1и A2. Эти отрезки пересекают S1и S2в точках B1и B2. Докажите, чтоA1A2|B1B2.
Решение
Проведем диаметр окружности S, являющийся осью симметрии окружностей S1и S2. Пусть точки C'и B2' симметричны точкам Cи B2относительно этого диаметра (рис.). Окружности S1и Sгомотетичны с центром гомотетии в точке A1, причем при этой гомотетии прямаяB1B2' переходит в прямуюCC', поэтому эти прямые параллельны. Ясно также, чтоB2B2'|CC'. Поэтому точки B1,B2' и B2лежат на одной прямой, причем эта прямая параллельна прямойCC'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет