Предположим, что прямая lпостроена. Рассмотрим окружность S₁', симметричную окружности S₁относительно точки A. Пусть O₁,O₁' и O₂ — центры окружностей S₁,S₁' и S₂(рис.). Проведем через точки O₁' и O₂прямые l₁' и l₂, перпендикулярные прямой l. Расстояние между прямыми l₁' и l₂равно половине разности длин хорд, высекаемых прямой lна окружностях S₁и S₂. Поэтому для построения прямой lнужно построить окружность радиуса a/2 с центром O₁'; прямая l₂будет касательной к этой окружности. Построив прямую l₂, опускаем на нее перпендикуляр из точки Aи получаем прямую l.

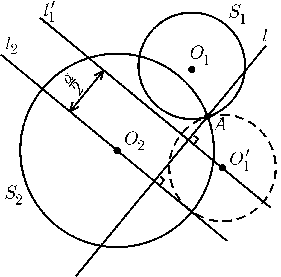
Ответ задачи отсутствует