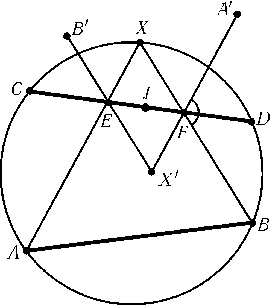
Задача
Даны непересекающиеся хордыABи CDокружности и точка Jна хордеCD. Постройте на окружности точку Xтак, чтобы хордыAXи BXвысекали на хордеCDотрезокEF, делящийся точкой Jпополам.
Решение
Предположим, что точка Xпостроена. Обозначим образы точек A,Bи Xпри симметрии относительно точки Jчерез A',B'и X'соответственно (рис.). Угол$\angle$A'FB= 180o-$\angle$AXBизвестен, поэтому точка Fявляется точкой пересечения отрезкаCDс дугой окружности, из которой отрезокBA'виден под углом180o-$\angle$AXB. Точка Xявляется точкой пересечения прямойBFс данной окружностью.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет