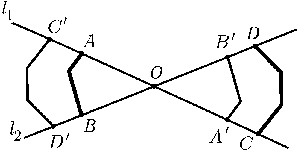
Рассмотрим многоугольник, симметричный исходному относительно точки O. Так как стороны многоугольника попарно непараллельны, контуры этих многоугольников не могут иметь общих отрезков, а могут иметь только общие точки. А так как многоугольники выпуклые, на каждой стороне лежит не более двух точек пересечения; поэтому имеется не более 2nточек пересечения контуров (точнее,nпар симметричных относительно Oточек). Пусть l₁и l₂ — прямые, проходящие через точку Oи делящие площадь исходного многоугольника пополам. Докажем, что внутри каждой из четырех частей, на которые эти прямые делят плоскость, есть точка пересечения контуров. Предположим, что в одной из частей между прямыми l₁и l₂нет таких точек. Обозначим точки пересечения прямых l₁и l₂со сторонами многоугольника так, как показано на рис. Пусть точки A',B',C'и D'симметричны относительно точки Oточкам A,B,Cи Dсоответственно. Для определенности будем считать, что точка Aлежит ближе к точке O, чем точка C'. Так как отрезкиABи C'D'не пересекаются, точка Bлежит ближе к точке O, чем точка D'. ПоэтомуS_ABO<S_C'D'O=S_CDO, гдеABO — выпуклая фигура, ограниченная отрезкамиAOи BOи частью границыn-угольника, заключенной между точками Aи B. С другой стороны,S_ABO=S_CDO, так как прямые l₁и l₂делят площадь многоугольника пополам. Получено противоречие. Поэтому между каждой парой прямых, делящих площадь пополам, лежит пара симметричных точек пересечения контуров, т. е. таких прямых не более n.

Ответ задачи отсутствует