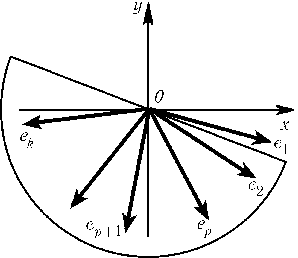
Можно считать, что сумма aданных векторов отлична от нуля, так как иначе утверждение задачи очевидно. Введем систему координат, направив ось Oyпо вектору a. Занумеруем векторы нижней полуплоскости по порядку — по часовой стрелке:e₁,e₂,... (рис.). По условию этих векторов не менее k. Докажем, что среди данных векторов найдутся еще такие векторыv₁,...,v_k, что для любогоi= 1,...,kвекторv_i+e_iимеет неположительную вторую координату. Этим будет доказано требуемое утверждение. В самом деле, длина суммы всех данных векторов равна сумме вторых координат (именно так была введена система координат). Сумма векторовe₁,v₁,...,e_k,v_kимеет неположительную вторую координату, а вторая координата любого из оставшихсяn- 2kвекторов не превосходит 1. Поэтому вторая координата суммы всех данных векторов не превосходитn- 2k. Пусть векторыe₁,...,e_pлежат в четвертом квадранте. Начнем сопоставлять им векторыv₁,...,v_p. Будем поворачивать нижнюю полуплоскость, состоящую из точек с неположительной второй координатой, поворачивая ось Oxпо часовой стрелке на угол от 0^oдо 90^o. Если один из двух векторов, лежащих в повернутой таким образом полуплоскости, расположен в четвертом квадранте, то их сумма имеет неположительную вторую координату. Как только при повороте плоскости ось Oxперейдет за вектор e₁, к векторамe₂,...,e_k, лежащим в ней, должен добавиться еще хотя бы один вектор; поэтому следующий за e_kпо порядку вектор можно взять в качестве v₁. Аналогично, когда ось Oxперейдет за вектор e₂, получим вектор v₂и т. д. Такие же рассуждения остаются справедливыми до тех пор, пока ось Oxостается в четвертом квадранте. Для векторовe_{p + 1},...,e_k, лежащих в третьем квадранте, доказательство проводится аналогично (если вектор e_{p + 1}имеет нулевую первую координату, то его следует сначала выбросить из рассмотрения, а затем в качестве парного к нему взять любой из оставшихся векторов).

Ответ задачи отсутствует