Задача
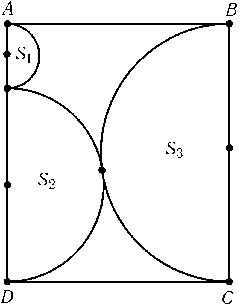
Центры окружностей с радиусами 1, 3 и 4 расположены на сторонах ADи BCпрямоугольника ABCD. Эти окружности касаются друг друга и прямых ABи CDтак, как показано на рис. Докажите, что существует окружность, касающаяся всех этих окружностей и прямой AB.
Решение
Пусть x — радиус окружности S, касающейся окружностей S1и S2и луча AB, y — радиус окружности S', касающейся окружностей S2и S3и луча BA. Положение окружности, касающейся окружности S1и луча AB(соответственно S3и луча BA) однозначно определяется ее радиусом, поэтому достаточно проверить, что x=y. Приравнивая два выражения для квадрата расстояния от центра окружности Sдо прямой AD, получаем (x+ 1)2- (x- 1)2= (3 +x)2- (5 -x)2, т. е. x= 4/3. Рассматривая окружности S2и S3, легко проверить, что AB2= (3 + 4)2- 12= 48. С другой стороны, квадраты расстояний от центра окружности S'до прямых ADи BCравны (y+ 3)2- (5 -y)2= 16(y- 1) и (4 +y)2- (4 -y)2= 16yсоответственно. Следовательно, 4$\sqrt{y-1}$+ 4$\sqrt{y}$=$\sqrt{48}$, т. е. y= 4/3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь