Задача
На отрезке ABвзята точка Cи на отрезках AC,BCи ABкак на диаметрах построены полуокружности, лежащие по одну сторону от прямой AB. Через точку Cпроведена прямая, перпендикулярная AB, и в образовавшиеся криволинейные треугольники ACDи BCDвписаны окружности S1и S2(рис.). Докажите, что радиусы этих окружностей равны.
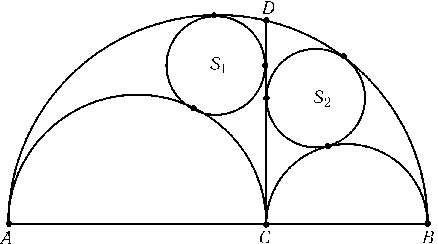
Решение
Пусть Pи Q — середины отрезков ACи AB, R — центр окружности S1; a=AC/2,b=BC/2, x — радиус окружности S1. Легко проверить, что PR=a+x,QR=a+b-xи PQ=b. Проведем в треугольнике PQRвысоту RH. Расстояние от точки Rдо прямой CDравно x, поэтому PH=a-x, а значит, QH= |b-a+x|. Следовательно, (a+x)2- (a-x)2=RH2= (a+b-x)2- (b-a+x)2, т. е. ax=b(a-x). В итоге получаем x=ab/(a+b). Для радиуса окружности S2получаем точно такое же выражение.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь