Задача
Даны две пересекающиеся окружности радиуса R, причем расстояние между их центрами больше R. Докажите, что β = 3α (рис.).
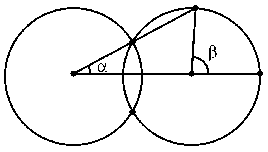
Решение
Пусть Aи B — вершины углов $\alpha$и $\beta$, P — точка пересечения несовпадающих сторон этих углов, Q — общая точка данных окружностей, лежащая на отрезке PA. Треугольник AQBравнобедренный, поэтому $\angle$PQB= 2$\alpha$. А так как $\angle$PQB+$\angle$QPB=$\beta$+$\angle$QBA, то $\beta$= 3$\alpha$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет