Назад
Задача 157617 • Сложность: 2 • 9 класс
Задача

Докажите, что

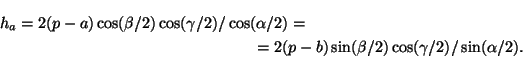
\begin{multline*} h_a=2(p-a)\cos(\beta /2)\cos(\gamma /2)/\cos(\alpha /2)=\\ =2(p-b)\sin(\beta /2)\cos(\gamma /2)/\sin(\alpha /2). \end{multline*}

Решение

Так как aha= 2S= 2(p-a)raи ra/a= cos($\beta$/2)cos($\gamma$/2)/cos($\alpha$/2) (задача 12.17, б)), то ha= 2(p-a)cos($\beta$/2)cos($\gamma$/2)/cos($\alpha$/2). Учитывая, что (p-a)ctg($\beta$/2) =rc= (p-b)ctg($\alpha$/2) (задача 12.17, в)), получаем ha= 2(p-b)sin($\beta$/2)cos($\gamma$/2)/sin($\alpha$/2).

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет