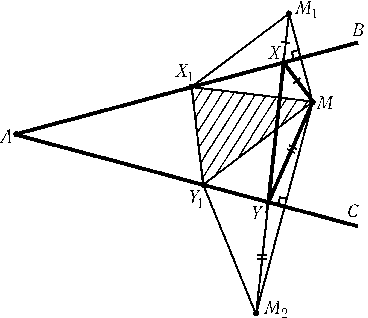
Пусть точки M₁и M₂симметричны Mотносительно прямыхABиAC. Так как$\angle$BAM₁=$\angle$BAMи$\angle$CAM₂=$\angle$CAM, то$\angle$M₁AM₂= 2$\angle$BAC< 180^o. Поэтому отрезокM₁M₂пересекает лучиABиACв некоторых точках Xи Y(рис.). Докажем, что Xи Y — искомые точки. В самом деле, если точки X₁и Y₁лежат на лучахABиAC, тоMX₁=M₁X₁иMY₁=M₂Y₁, т. е. периметр треугольникаMX₁Y₁равен длине ломанойM₁X₁Y₁M₂. Из всех ломаных с концами в точках M₁и M₂наименьшую длину имеет отрезокM₁M₂.

Ответ задачи отсутствует