Задача
Дан уголXAYи точка Oвнутри его. Проведите через точку Oпрямую, отсекающую от данного угла треугольник наименьшей площади.
Решение
Рассмотрим уголX'A'Y', симметричный углуXAYотносительно точки O. Пусть Bи C — точки пересечения сторон этих углов. Обозначим точки пересечения прямой, проходящей через точку O, со сторонами угловXAYиX'A'Y'через B1,C1и B1',C1' соответственно (рис.). Так какSAB1C1=SA'B1'C1', тоSAB1C1= (SABA'C+SBB1C1'+SCC1B1')/2. Площадь треугольникаAB1C1минимальна, еслиB1=BиC1=C, т. е. искомой прямой являетсяBC.
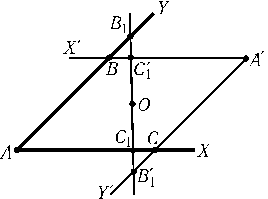
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет