Задача
Точки A1, B1 и C1 взяты на сторонах BC, CA и AB треугольника ABC, причём отрезки AA1, BB1 и CC1 пересекаются в одной точке M.
При каком положении точки M величина MA1/AA1·MB1/BB1·MC1/CC1 максимальна?
Решение
Пусть u = MA1/AA1, v = MB1/BB1, w = MC1/CC1. Так как u + v + w = 1
(см. задачу 156799, а)), то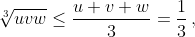 
причём равенство достигается, когда u = v = w = ⅓,
то есть M – точка пересечения медиан.
Ответ
Когда M – точка пересечения медиан.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет