Задача
На гипотенузе AB прямоугольного треугольника ABC взята точка X, M и N – её проекции на катеты AC и BC.
а) При каком положении точки X длина отрезка MN будет наименьшей?
б) При каком положении точки X площадь четырёхугольника CMXN будет наибольшей?
Решение
а) Так как CMXN – прямоугольник, то MN = CX. Поэтому длина отрезка MN будет наименьшей, если CX – высота. б) Пусть SABC = S. Тогда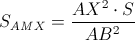 
и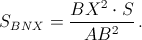 
Поскольку AX² + BX² ≥ ½ AB² (причём равенство достигается, только когда X – середина отрезка AB), то SCMXN = S – SAMX – SBNX ≤ S/2.
Ответ
а) Когда X – основание высоты.
б) Когда X – середина отрезка AB.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет