Пусть  f = bccosx + cacosy + abcosz.  Так как  cosx= – cosycosz+ sinysinz,  то  f = c(a – bcosz) cosy + bcsinysinz + abcosz.   Рассмотрим треугольник, длины двух сторон которого равныaиb, а угол между ними равенz; пусть φ и ψ – углы, лежащие против сторонaиb,

t– длина стороны, лежащей против углаz. Легко видеть, что  a – bcosz=tcos ψ,  а  bsinz = tsin ψ.  Следовательно, f = ctcos ψ cosy + ctsinysin ψ +abcosz = ctcos(ψ –y) + ½ (a² +b² –t²).   Так как  cos(ψ –y) ≤ 1,  то  f≤ ½ (a² +b² +c²).  Так как  a ≥ b,  то  φ ≥ ψ,  а значит,  – φ ≤ – ψ <y– ψ < π –z– ψ = φ,  то есть cos(y– ψ) > cos φ.  Поэтому

 

 

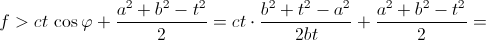
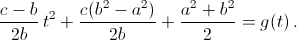
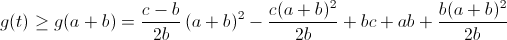
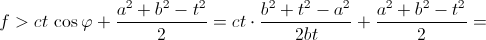
Ответ задачи отсутствует