Задача
Площадь треугольникаABCравна 1. Пусть A1,B1,C1 — середины сторонBC,CA,ABсоответственно. На отрезкахAB1,CA1,BC1взяты точки K,L,Mсоответственно. Чему равна минимальная площадь общей части треугольниковKLMи A1B1C1?
Решение
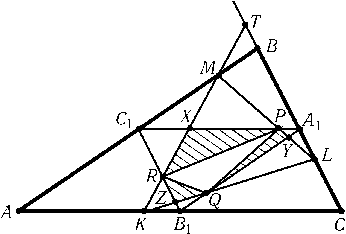
Обозначим точку пересечения прямыхKMиBCчерез T, а точки пересечения сторон треугольниковA1B1C1иKLMтак, как показано на рис. ТогдаTL:RZ=KL:KZ=LC:ZB1. Так какTL$\ge$BA1=A1C$\ge$LC, тоRZ$\ge$ZB1, т. е.SRZQ$\ge$SZB1Q. АналогичноSQYP$\ge$SYA1Pи SPXR$\ge$SXC1R. Складывая все эти неравенства и неравенствоSPQR$\ge$0, получаем, что площадь шестиугольникаPXRZQYне меньше площади оставшейся части треугольникаA1B1C1, т. е. его площадь не меньшеSA1B1C1/2 = 1/8. Равенство достигается, например, если точка Kсовпадает с B1, а точка M — с B.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь