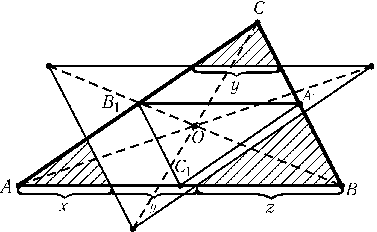
Пусть O — центр симметрии многоугольника M, расположенного внутри треугольника T,S(T) — образ треугольника Tпри симметрии относительно точки O. Тогда Mлежит и в T, и в S(T). Поэтому среди всех центрально симметричных многоугольников с данным центром симметрии, лежащих в T, наибольшую площадь имеет пересечение Tи S(T). Точка Oлежит внутри треугольника T, так как пересечением Tи S(T) является выпуклый многоугольник, а выпуклый многоугольник всегда содержит свой центр симметрии. Пусть A₁,B₁и C₁ — середины сторонBC,CAиABтреугольникаT=ABC. Предположим сначала, что точка Oлежит внутри треугольникаA₁B₁C₁. Тогда пересечением Tи S(T) является шестиугольник (рис.). Пусть сторонаABделится сторонами треугольникаS(T) в отношенииx:y:z, гдеx+y+z= 1. Тогда отношение суммы площадей заштрихованных треугольников к площади треугольникаABCравноx²+y²+z²; нужно минимизировать это выражение. Так как1 = (x+y+z)²= 3(x²+y²+z²) - (x-y)²- (y-z)²- (z-x)², тоx²+y²+z²$\ge$1/3, причем равенство достигается только приx=y=z; последнее равенство означает, что O — точка пересечения медиан треугольникаABC. Рассмотрим теперь другой случай: точка Oлежит внутри одного из треугольниковAB₁C₁,A₁BC₁,A₁B₁C, например внутри$\triangle$AB₁C₁. В этом случае пересечением Tи S(T) является параллелограмм, причем если мы заменим точку Oточкой пересечения прямыхAOиB₁C₁, то площадь этого параллелограмма может только увеличиться. Если же точка Oлежит на сторонеB₁C₁, то этот случай уже фактически был нами рассмотрен (нужно положитьx= 0). Искомым многоугольником является шестиугольник с вершинами в точках, делящих стороны треугольника на три равные части. Его площадь равна 2/3 площади треугольника.

Ответ задачи отсутствует