Назад
Задача 157443 • Сложность: 5 • 8-9 класс
Задача

Докажите, что а) 5R-r$\geq$$\sqrt{3}$p; б) 4R-ra$\geq$(p-a)[$\sqrt{3}$+ (a2+ (b-c)2)/(2S)].

Решение

а) Сложив равенство 4R+r=ra+rb+rc(задача 12.24) с неравенством R- 2r$\geq$0 (задача 10.26), получим

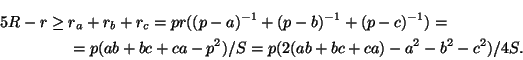
\begin{multline*} 5R-r\geq r_a+r_b+r_c= pr((p-a)^{-1}+(p-b)^{-1}+(p-c)^{-1})=\\ =p(ab+bc+ca-p^2)/S= p(2(ab+bc+ca)-a^2-b^2-c^2)/4S. \end{multline*}

Остается заметить, что 2(ab+bc+ac) -a2-b2-c2$\geq$4$\sqrt{3}$S(задача 10.54). б) Легко проверить, что 4R-ra=rb+rc-r=pr/(p-b) +pr/(p-c) -pr/p= (p-a)(p2-bc)/S. Остается заметить, что 4(p2-bc) =a2+b2+c2+ 2(ab-bc+ca) = 2(ab+bc+ac) -a2-b2-c2+ 2(a2+b2+c2- 2bc)$\geq$4$\sqrt{3}$S+ 2(a2+ (b-c)2).

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет