Назад
Задача 157426 • Сложность: 4 • 8-9 класс
Задача

Докажите, что ha/la$\geq$$\sqrt{2r/R}$.

Разделы:
Планиметрия
Источники:
Прасолов В.В., Задачи по планиметрии глава 10. Неравенства для элементов треугольника параграф 3. Биссектрисы Книги, журналы
Количество версий:
3
Решение

Ясно, что ha/la= cos(($\beta$-$\gamma$)/2). Согласно задаче 12.36, а)

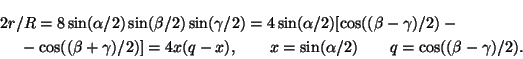
\begin{multline*} 2r/R=8\sin(\alpha /2)\sin(\beta /2)\sin(\gamma /2)=4\sin(\alp... ...sin(\alpha /2) \quad \text{и}\quad q=\cos((\beta -\gamma )/2). \end{multline*}

Остается заметить, что 4x(q-x)$\leq$q2.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет