Задача
Отрезок KLпроходит через точку пересечения диагоналей четырехугольника ABCD, а концы его лежат на сторонах ABи CD. Докажите, что длина отрезка KLне превосходит длины одной из диагоналей.
Решение
Проведем через концы отрезка KLпрямые, ему перпендикулярные, и рассмотрим проекции на них вершин четырехугольника, а также точки пересечения с ними прямых ACи BD(рис.). Пусть для определенности точка Aлежит внутри полосы, заданной этими прямыми, а точка B — вне ее. Тогда можно считать, что Dлежит внутри полосы, так как иначе BD>KL, и доказательство завершено. Так как
$\displaystyle \leq$ $\displaystyle {\frac{A_1K}{B_1K}}$ = $\displaystyle {\frac{C_1L}{D_1L}}$ $\displaystyle \leq$ 
,
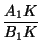
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет