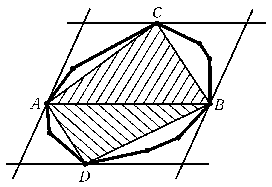
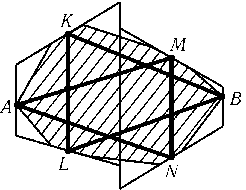
а) Заключим многоугольник в полосу, образованную параллельными прямыми. Будем сдвигать эти прямые параллельно до тех пор, пока на каждую из них не попадут некоторые вершины Aи Bмногоугольника. Затем проделаем то же самое для полосы, образованной прямыми, параллельными AB. На эти прямые попадут некоторые вершины Cи D(рис.). Исходный многоугольник заключен в параллелограмм, поэтому площадь этого параллелограмма не меньше 1. С другой стороны, сумма площадей треугольников ACBи ADBравна половине площади параллелограмма, поэтому площадь одного из этих треугольников не меньше 1/4.

б) Как и в задаче а), заключим многоугольник в полосу, образованную параллельными прямыми, так, чтобы вершины Aи Bлежали на этих прямых (рис.). Пусть ширина этой полосы равна d. Проведем три прямые, делящие эту полосу на равные полосы шириной d/4. Пусть первая и третья прямые пересекают стороны многоугольника в точках K,Lи M,Nсоответственно. Продолжим стороны, на которых лежат точки K,L,Mи N, до пересечения со сторонами исходной полосы и с прямой, делящей ее пополам. При этом образуются две трапеции со средними линиями KLи MN, высоты которых равны d/2. Так как эти трапеции покрывают весь многоугольник, сумма их площадей не меньше его площади, т. е. (d ^. KL+d ^. MN)/2$\geq$1. Сумма площадей треугольников AMNи BKL, содержащихся в исходном многоугольнике, равна (3d ^. MN+ 3d ^. KL)/8$\geq$3/4. Поэтому площадь одного из этих треугольников не меньше 3/8.

Ответ задачи отсутствует