Задача
Докажите, что если в выпуклом шестиугольнике каждый из трех отрезков, соединяющих середины противоположных сторон, делит площадь пополам, то эти отрезки пересекаются в одной точке.
Решение
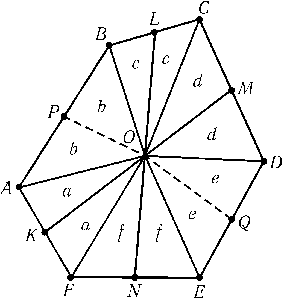
Обозначим середины сторон выпуклого шестиугольника ABCDEFтак, как показано на рис. Пусть O — точка пересечения отрезков KMи LN. Площади треугольников, на которые делят шестиугольник отрезки, соединяющие точку Oс вершинами и серединами сторон, обозначим так, как показано на том же рисунке. Легко проверить, что SKONF=SLOMC, т. е. a+f=c+d. Следовательно, ломаная POQделит шестиугольник на две части равной площади, а значит, отрезок PQпроходит через точку O.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет