Задача
Противоположные стороны выпуклого шестиугольника ABCDEFпопарно параллельны. Докажите, что: а) площадь треугольника ACEсоставляет не менее половины площади шестиугольника. б) площади треугольников ACEи BDFравны.
Решение
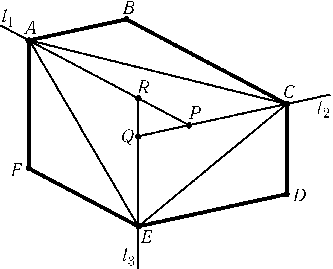
Проведем через точки A,Cи Eпрямые l1,l2и l3, параллельные прямым BC,DEи FAсоответственно. Обозначим точки пересечения прямых l1и l2, l2и l3, l3и l1через P,Q,Rсоответственно (рис.). Тогда
SACE = (SABCDEF - SPQR)/2 + SPQR = (SABCDEF + SPQR)/2 $\displaystyle \geq$ SABCDEF/2.
Аналогично SBDF= (SABCDEF+SP'Q'R')/2. Ясно, чтоPQ= |AB-DE|,QR= |CD-AF|,PR= |EF-BC|,
поэтому треугольники PQRи P'Q'R'равны. Следовательно, SACE=SBDF.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет