Задача
Окружности радиуса xи yкасаются окружности радиуса R, причем расстояние между точками касания равно a. Вычислите длину следующей общей касательной к первым двум окружностям: а) внешней, если оба касания внешние или внутренние одновременно; б) внутренней, если одно касание внутреннее, а другое внешнее.
Решение
Пусть оба касания внешние и x$\leq$y. Прямая, проходящая через центр Oокружности радиусаxпараллельно отрезку, соединяющему точки касания, пересекает окружность радиуса y-x(с центром в центре окружности радиуса y) в точках Aи B(рис.). Тогда OA=a(R+x)/Rи OB=OA+a(y-x)/R=a(R+y)/R. Квадрат искомой длины общей внешней касательной равен
OA . OB = (a/R)2(R + x)(R + y).
Аналогичные рассуждения показывают, что если оба касания внутренние, то
квадрат длины внешней касательной равен (a/R)2(R-x)(R-y), а если
окружность радиуса xкасается внешне, а окружность радиуса y —
внутренне, то квадрат длины внутренней касательной
равен (a/R)2(R-y)(R+x).
Замечание.
В случае внутреннего касания окружностей предполагается, что R>xи R>y.
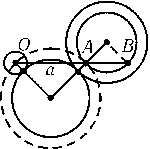
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет