Задача
Четырехугольник ABCDвыпуклый; точки A1,B1,C1и D1таковы, что AB||C1D1,AC||B1D1и т. д. для всех пар вершин. Докажите, что четырехугольник A1B1C1D1тоже выпуклый, причем $\angle$A+$\angle$C1= 180o.
Решение
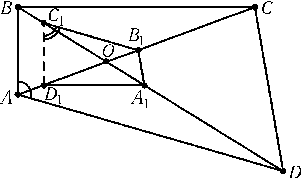
Любой четырехугольник с точностью до подобия определяется направлениями своих сторон и диагоналей (см. задачу157035), поэтому достаточно построить один пример четырехугольника A1B1C1D1с требуемыми направлениями сторон и диагоналей. Пусть O — точка пересечения диагоналей ACи BD. На луче OAвозьмем произвольную точку D1и проведем D1A1||BC,A1B1||CDи B1C1||DA(см. рис.). Так как OC1:OB1=OD:OA,OB1:OA1=OC:ODи OA1:OD1=OB:OC, то OC1:OD1=OB:OA, а значит, C1D1||AB. Из полученного рисунка ясно, что $\angle$A+$\angle$C1= 180o.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь