Задача
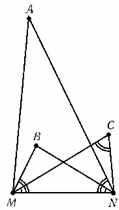
На отрезке MN построены подобные, одинаково ориентированные треугольники AMN, NBM и MNC (см. рис.).
Докажите, что треугольник ABC подобен всем этим треугольникам, а центр его описанной окружности равноудален от точек M и N.
Решение
Так как ∠AMN = ∠MNC и ∠BMN = ∠MNA, то ∠AMB = ∠ANC. Кроме того, AM : AN = NB : NM = BM : CN. Поэтому треугольники AMB и ANC подобны, а значит, ∠MAB = ∠NAC. Следовательно, ∠BAC = ∠MAN. Для других углов доказательство аналогично.
Заметим, что прямая CN симметрична прямой AM, прямая BM – прямой AN, а прямая BN – прямой CM относительно серединного перпендикуляра к отрезку MN. Значит, точка B1 пересечения прямых MC и AN симметрична точке B относительно этого перпендикуляра. Аналогично точка C1 пересечения прямых NB и AM симметрична точке C.
Так как AM : NB = MN : BM = MC : NC, то MA·MC1 = AM·NC = NB·MC = MB1·MC. Следовательно, точка A лежит на окружности, описанной вокруг трапеции BB1CC1. Центр этой окружности лежит на указанном серединном перпендикуляре.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь