Задача
Через произвольную точку P стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.
Решение
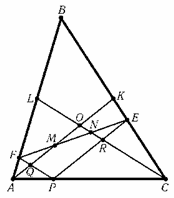
Обозначим точку пересечения медиан через O, точки пересечения медианы AK с прямыми FP и FE – через Q и M, точки пересечения медианы CL с прямыми EP и FE – через R и N соответственно (см. рис.). FM : FE = FQ : FP = LO : LC = 1 : 3, то есть FM = FE/3. Аналогично EN = FE/3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет