Задача
Длины двух сторон треугольника равны a, а длина третьей стороны равна b. Вычислите радиус его описанной окружности.
Решение
Пусть O – центр описанной окружности равнобедренного треугольника ABC, B1 – середина основания AC, A1 – середина боковой стороны BC. Так как треугольники BOA1 и BCB1 подобны, то BO : BA1 = BC : BB1, а значит, R = BO = 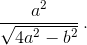
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет